Suppose that you deposit $100 in the bank. If the interest rate is 10% per year (compounded daily) and you wait 100 years what will happen? This is an example of a first order positive feedback loop.

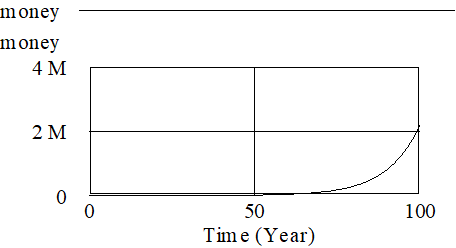
At the end of 100 years there would be over two million dollars in the bank. Exponential growth is interesting because it demonstrates a constant doubling time. If it takes, as it does in this example, about 7 years to go from 100 to 200 dollars, it will also take about 7 years to go from 1 million to 2 million dollars. It is a useful exercise to explore the relationship between the interest rate and the time it takes the money to double.
Note that for this example you can either select TIME STEP to be small enough (about .125) so that it makes no difference or choose Runge-Kutta integration.