(mice.mdl)
Suppose that you let some mice loose in your house and don't try to kill them. What will happen to the mouse population? At first glance this sounds very much like the exponential growth example, and for the first little time it is. Try as they might, though, the mice will never get 2 million of themselves into your house.

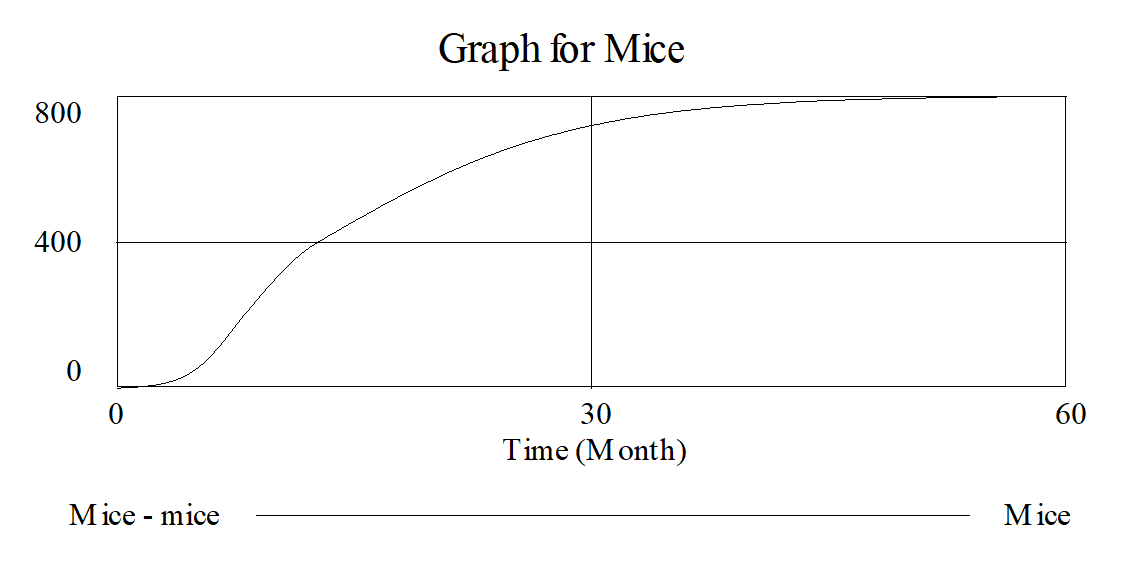
The beginning of this does indeed look like exponential growth while the end looks like exponential adjustment. To get this kind of transition there has to be more than a single feedback loop operating. Often, and in the case of this simple model, there are both a positive and negative feedback loop with the positive loop dominate in the beginning and the negative loop dominant in the end.
It is interesting to experiment with the Constant max net new mice rate to see the effect this has. Watching the way net new mice behaves as you change values is especially interesting. The process of adjustment in this model is almost entirely dependent on the shape of the Lookup effect of density on survival function. Experimenting with different shapes for this function can also be interesting.