This chapter is a detailed discussion of the Vensim modeling language, which allows for simple representation of complex dynamic systems. For the discussion that follows it is important to understand that it is the Levels (or state variables) that define the dynamics of a system. For the mathematically inclined we can introduce this in a more formal way. The following equations show the basic mathematical form of the Vensim modeling language.
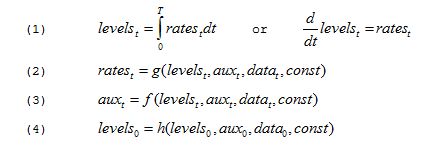
In these equations g, h, and f are arbitrary, nonlinear, potentially time varying, vector-valued functions. Equation 1 represents the evolution of the system over time, equation 2 the computation of the rates determining that evolution, equation 3 the intermediate results necessary to compute the rates, and equation 4 the initialization of the system.
Equation 1 above is written using both integral and differential notation. The format that Vensim uses for expressing equations matches more closely the first, but the two equations have the same meaning.
Equation 3 above could also be written as:
In this notation the implicit solution to the above equation defines auxt. We do not use this notation because Vensim allows elements of auxt to depend on other elements, but not normally in a circular fashion (see "Causal Models" below).Vensim does have the functionality to solve special cases of equation 3a, (see "Simultaneous Equations" below) but this functionality is not part of the standard system dynamics framework.