One of the principles of economic theory is that price will adjust so that supply and demand match. This way of thinking about allocation actually turns out to be very useful even for situations where price adjustment is not used as a market clearing mechanism. To understand this, we start with a pure supply and demand example and see how the approach can be used to solve the JoeBob versus GM problem discussed earlier.
Suppose that there are two suppliers with the supply curves shown below:

and that there are two demander with the demand curves shown below:
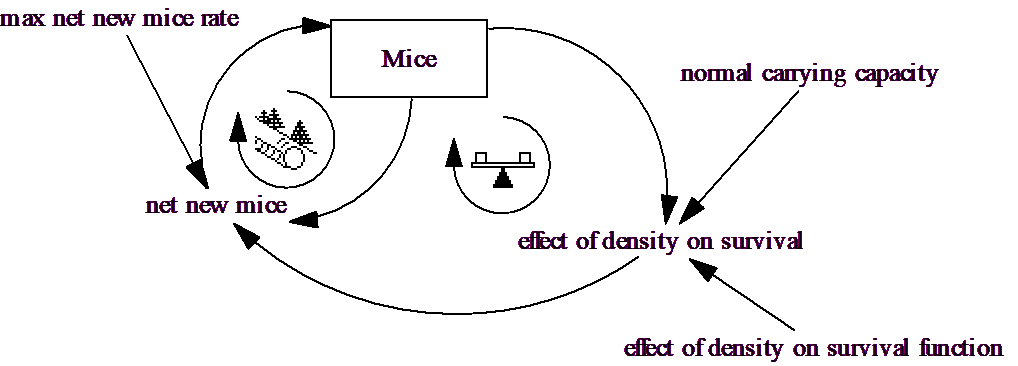
We can find a market equilibrium by adding up the two supply curves to form a market supply curve, adding up the two demand curves to form a market demand curve, and then finding the point where the two curves intersect.
Once we find that price, about 7, we just go back to the original supply and demand curves to determine how much each supplier supplies, and how much each demander demands.
Consider again the original example of car sales. In this case we said that there is some market demand and we want to determine how it is divided between the two suppliers. Thus we treat the market demand as constant, determine the price where it intersects the supply curves.
If the demand is small, such as at d1, only supplier s2 supplies anything. At demand d2 both suppliers supply something. If the demand is d3, supply never meets demand so we can’t determine price. It is clear, however, that both suppliers should supply all they can.
In the earlier section we were talking about priority, and now we are talking about price. While the two seem related, they are not the same thing. In fact as the example was posed the decision about what to buy was a decision by demanders based on preference not a decision by suppliers based on price. However, all we need to do is flip the supply curve and change the label on the x axis to get that interpretation:

If demand is low (d1), the highest priority suppliers are used. When demand is higher (d2), more suppliers are used. If the demand is very high (d3) then all suppliers are used to their capacities.
What we have created then, is a graphical way of solving the one-to-many or many-to-many allocation problem. We can interpret this as either a market based balancing of supply and demand, or a rationing scheme based on the preferences of the agent being rationed to. The underlying curves can be made to respect the capacities of the agents, and the preferences of agents can me represented by selecting different shapes and positions.
This approach is a generalization of the approach and algorithm developed by William T. Wood in the 1980s to solve the one-to-many allocation problem using prioritization curves such as the ones illustrated above.