In addition to keeping track of how long something has waited in a queue, it is often useful to understand the distribution of attributes within the queue. In discrete event simulation the approach is to take individual entities and track them as they function within a system. Sometimes it makes sense to go to that level of detail using subscripts, but sometimes something a little bit less detailed is called for. Using queues with attributes allows you to get to somewhat more detail without the full machinery of subscripts.
As an example consider keeping track of the gas mileage of different vintages of cars. The typical continuous approach to this problem would be to use what is called a coflow as is shown here (queue3.mdl).
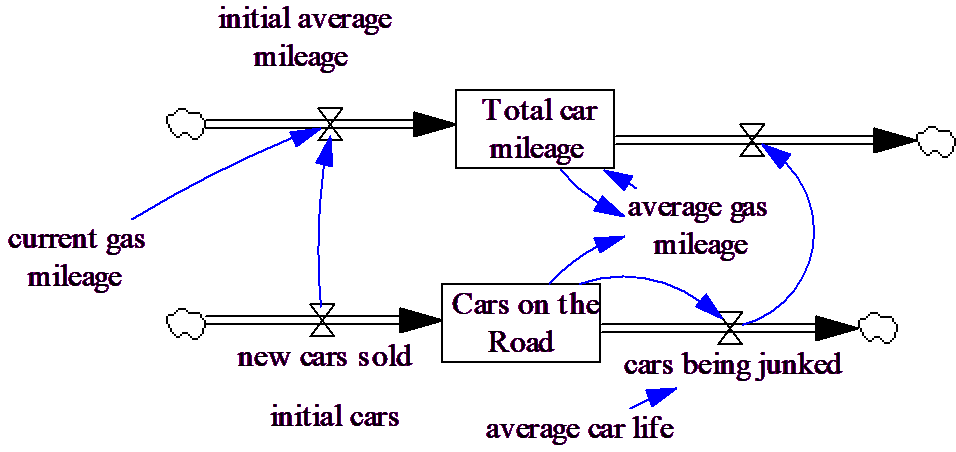
In a coflow the attribute is tracked in a separate level with units of measure Car*Mile/Gallon.
The coflow operates on a negative exponential residence distribution rather than a FIFO approach. Formulated using FIFO queues the model would become (queue4.mdl):
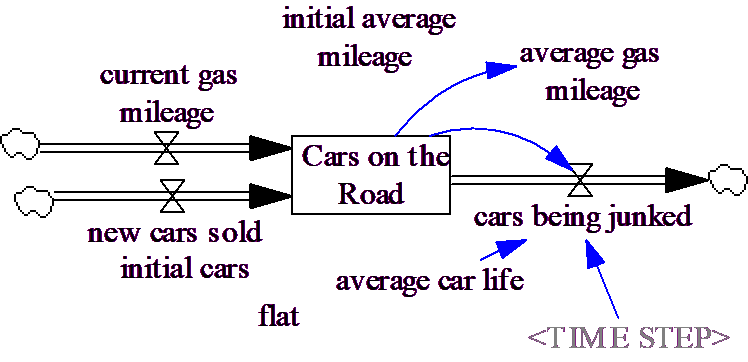
We have removed the abstract level total car mileage, and now show two flows into Cars on the Road. One of these flows is really the flow of an attribute, but this seems the clearest representation. The equation for Cars on the Road becomes:
| Cars on the Road = QUEUE FIFO ATTRIB( new cars sold, |
| cars being junked, current gas mileage, 0, flat, flat, |
| initial cars, initial average mileage, average car life) |
This equation is really taking two level equations and computing them at the same time. The average gas mileage is now computed using the formula
| average gas mileage= |
| QUEUE ATTRIB AVERAGE(Cars on the Road, -1) |
Finally the equation for cars being junked is replaced by:
| cars being junked=QUEUE AGE IN RANGE(Cars on the Road, |
| average car life, 1e+009)/TIME STEP |
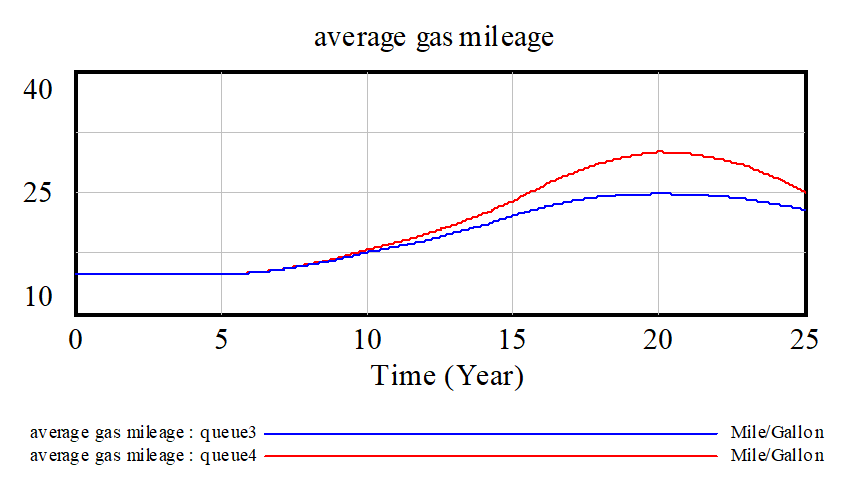
Looking at average gas mileage we see that there is significant difference between the two models:
An, of course there is a difference in Cars on the Road:

Unlike the cycle time computation, however, one of these is not clearly more right than the other. Both represent approximations. Cars are retired with neither a negative exponential distribution nor as a FIFO queue process.