This section is optional and produces a model with the same behavior as the rabbit.mdl model already constructed.
Lookup tables are best used to drive model variables above or below their "normal" values. In the previous model (rabbit.mdl), the normal value was implicit and hidden within the Rate equation for deaths. In other models, you might want to have an explicit normal value. This might be a Constant, or an Auxiliary as normal death rate in the rabbit2.mdl model below:
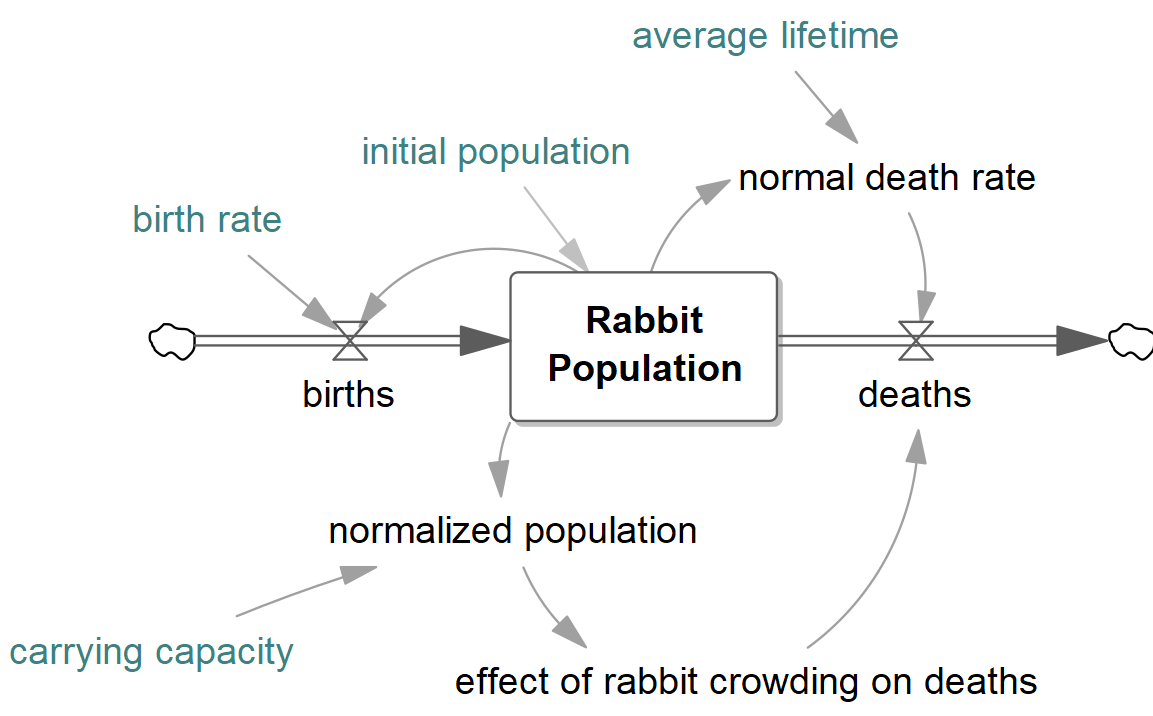
This model also includes an explict (separated) normalized input, rather than normalizing the input variable inside the variable effect of rabbit crowding on deaths.
| Ø | Save the previous rabbit model as another name (rabbit2.mdl) and then create the structure above. |
| Ø | To move the arrows from the Rate deaths to the Auxiliary normal death rate, use the Move/Size tool to grab the arrowhead from deaths and drop it on the Auxiliary. Alternatively, you can delete the arrows using the Delete tool by clicking on the arrowhead, then draw new arrows with the Arrow tool. |
| Ø | Click on normal death rate and enter the following equation (the same equation for deaths before we introduced the effect from the Lookup) and units then press Enter: |
| Rabbit Population / average lifetime |
Units: rabbit/Year
| Ø | Click on deaths and replace the equation with the one below then press Enter. |
| normal death rate * effect of rabbit crowding on deaths |
| Ø | Click on normalized populationand enter the equation below: |
| Rabbit Population / carrying capacity |
Units: Dmnl
| Ø | Click on effect of rabbit crowding on deaths and replace the equation in the WITH LOOKUP editing box with (leaving the Lookup table and units as they are): |
| effect of rabbit crowding on deaths= WITH LOOKUP ( |
The Equation Editor should close and no variables on the diagram should have highlights.
| Ø | Click on the Save button on the Toolbar to save your model. |
Note that the normal output variable normal death ratecould (in a different model) be a Constant, and not the Auxiliary that it is here. See for example, the structure below:
