Regardless of which hypothesis we consider, we need to think about how many people are using the technology. The process starts with the work of several people, then spreads. Holding this very simple thought we can start with:

There are two pools of people: Practitioners and Non Practitioners (we do our best to keep the language neutral here). These people are all going to conferences, attending meetings and bumping into one another on the street. Since the process of adoption requires that someone instill the idea of the technology into someone else, we are interested in the frequency with which someone who is not a practitioner encounters someone who is a practitioner. Therefore we start with non practitioner contacts with anyone, and then multiply by the fraction of people who are practitioners.
practitioner with non practitioner contacts represents contacts between someone who is practicing and someone who is not practicing. There is a chance that, as the result of this meeting, the non practitioner will take up practice. The probability that this happens is called the adoption fraction.
The equations for the above model are:
adoption fraction = 0.005
Units: Dmnl
| adoptions = practitioner with non practitioner contacts * |
| adoption fraction |
Units: Person/Year
contact rate = 100
Units: 1/Year
initial practitioners = 10
Units: Person
non practitioner contacts = Non Practitioners * contact rate
Units: Person/Year
| Non Practitioners = INTEG( |
| - adoptions, |
| 1e+007) |
Units: Person
Note that we start the model with 10 million people. This is intended to represent the number of academics and skilled professionals for whom this type of work is relevant. This number is an open issue for discussion, though we will not be addressing it in this chapter.
practitioner prevalence = Practitioners/total population
Units: Dmnl
| practitioner with non practitioner contacts = |
| non practitioner contacts * practitioner prevalence |
Units: Person/Year
| Practitioners = INTEG( |
| adoptions, |
| initial practitioners) |
Units: Person
total population = Non Practitioners + Practitioners
Units: Person
The model is run from the year 1960 to the year 2010 with TIME STEP at .125. This model generates the following behavior:
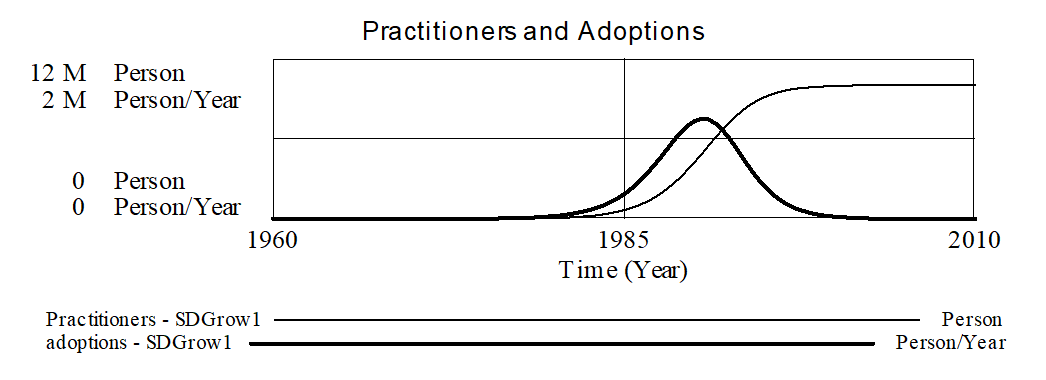
The behavior of the model is quite sensitive to the parameters chosen. For example, if we let adoption fraction taken on the values .01, .005 and .0025 we get:
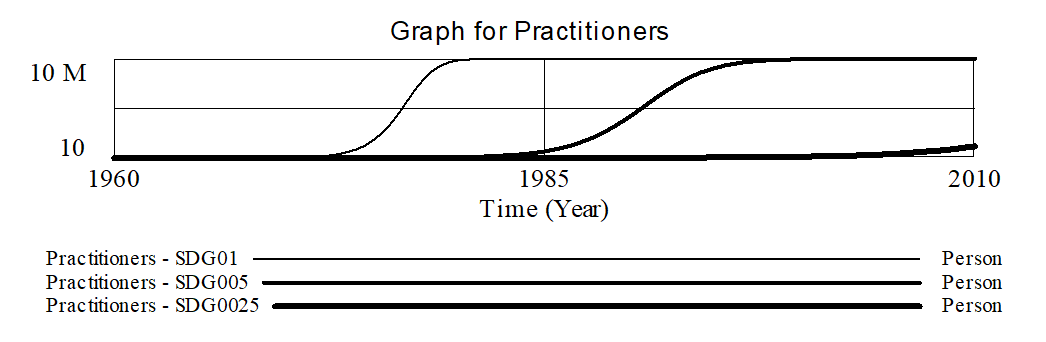
For higher values like .01, the number of practitioners grows rapidly and saturates early as the total population adopts the method. On the other hand, for a value of .0025 the number of practitioners barely registers on this scale. One interesting experiment to do is to lower the adoption fraction even further to .001 and see how long it takes before saturation occurs.