We have seen how important the adoption rate is: if it is too low, a technology will take so long to diffuse that it is likely to be lost in the wash of other events and technologies. The way we have modeled it, however, adoption is just a matter of picking up the tool and going to work. This is not, unfortunately, the way life works. After deciding that a technology is good and worth pursuing, it is necessary to spend time and effort to become capable enough to use the technology.
Instead of just looking at Non Practitioners and Practitioners, we can look at Non Practitioners, Training Practitioners, New Practitioners and Experienced Practitioners. Practitioners can then be reformulated as the sum of New Practitioners and Experienced Practitioners. Experienced Practitioners can also provide teaching and training to speed the transition from Training Practitioners to New Practitioners to Experienced Practitioners.
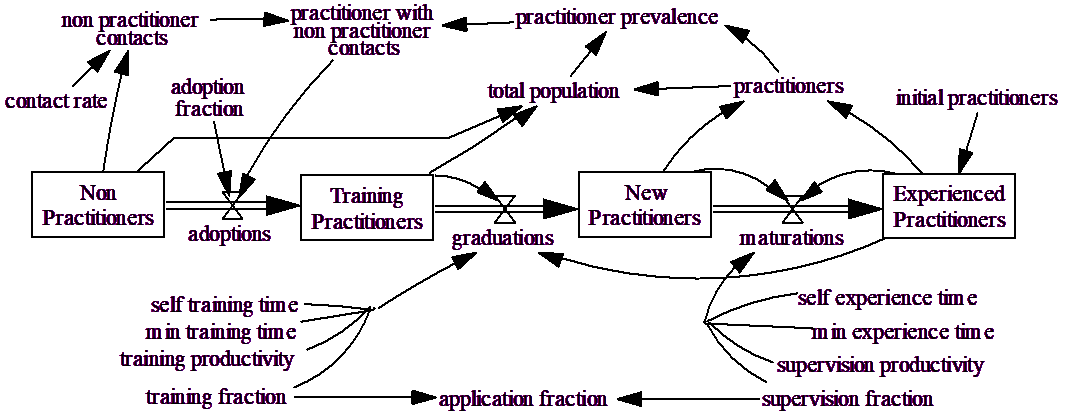
This diagram is a little bit busier, but is the same basic structure as the first model. There are six constants that determine the speed with which people can move through training and gaining experience. self training time is the time required for a person with no formal training to become sufficiently proficient to be a practitioner. min training time is the time required for a person with lots of formal training to become proficient. As Experienced Practitioners devote time to training, the average training time moves from self training time, to min training time according to training productivity. The formulation for people becoming experienced is exactly parallel.
The equations for this model are:
adoption fraction = 0.005
Units: Dmnl
| adoptions = practitioner with non practitioner contacts * |
| adoption fraction |
Units: Person/Year
| application fraction = INITIAL(1 - supervision fraction - |
| training fraction) |
Units: Dmnl
This represents the fraction of time experienced people devote to application (doing research, publishing and helping solve problems) and not training others. This is not used in this model, but will be used in the next refinement.
contact rate = 100
Units: 1/Year
Experienced Practitioners = INTEG(maturations,initial practitioners)
Units: Person
| graduations = MIN(Training Practitioners/min training time, |
| Training Practitioners/self training time + Experienced Practitioners * training fraction * training productivity) |
Units: Person/Year
Any addition of people devoted to training immediately adds to graduations until people are coming out as fast as they can be expected to at which point adding more trainers has no effect.
initial practitioners = 10
Units: Person
| maturations = MIN(New Practitioners/min experience time, |
| New Practitioners/self experience time + Experienced Practitioners * supervision fraction * supervision productivity) |
Units: Person/Year
min experience time = 1
Units: Year
min training time = 0.25
Units: Year
| New Practitioners = INTEG( |
| graduations - maturations, |
| 0) |
Units: Person
non practitioner contacts = Non Practitioners * contact rate
Units: Person/Year
| Non Practitioners = INTEG( |
| - adoptions, |
| 1e+007) |
Units: Person
practitioner prevalence = practitioners/total population
Units: Dmnl
| practitioner with non practitioner contacts = |
| non practitioner contacts * practitioner prevalence |
Units: Person/Year
practitioners = New Practitioners + Experienced Practitioners
Units: Person
self experience time = 4
Units: Year
self training time = 2
Units: Year
supervision fraction = 0
Units: Dmnl
supervision productivity = 4
Units: 1/Year
The supervision productivity is the number of people per year an experienced practitioner can train. Thus the units are (Person/Year)/Person or 1/Year.
| total population = Non Practitioners + Training Practitioners + |
| practitioners |
Units: Person
training fraction = 0
Units: Dmnl
| Training Practitioners = INTEG( |
| adoptions - graduations, |
| 0) |
Units: Person
training productivity = 20
Units: 1/Year
If we simulate this model at the three extremes, with application fraction = 1 (all effort is devoted to work in the field, and new practitioners must train themselves), training fraction = 1 (all effort is devoted to training novices) and supervision fraction = 1 (all effort is devoted to generating experienced practitioners) we get the following behavior:
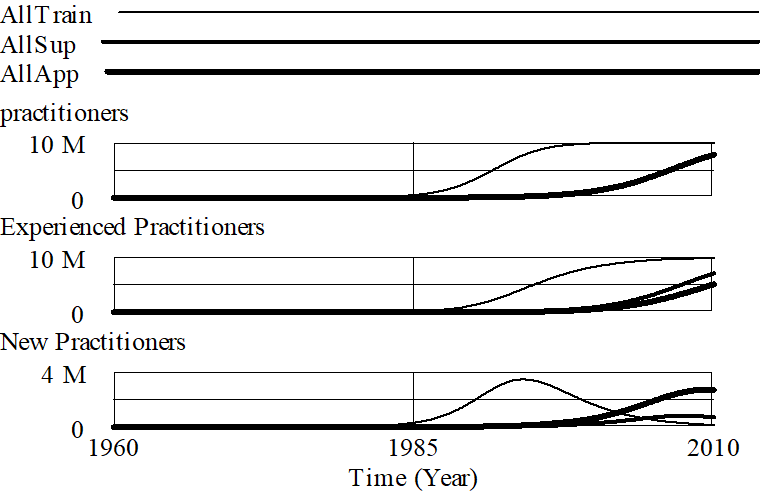
Devoting all attention to supervision or application both result in a much slower growth and saturation, with the only difference being in the fraction of the people who are experienced. If experienced people spend all their time training new practitioners then a big fraction of practitioners are going to be experienced, but since experienced people do nothing but make more experienced people no useful work comes of it.
If experienced people spend all their time training novices, there is a profound effect on the growth of the field. People who express interest can quickly become proficient and start using the technology. While this is an interesting result, it also suggests a deficiency in the model. If experienced people are only doing training, then all the work being done is being done by New Practitioners who are not likely to perform as well as experienced practitioners.