The willingness of people to adopt a new technology depends on a number of things including the difficulty of learning the technology, the expected benefits and the compatibility of the technology with existing technologies. While it is important to have lots of people espousing the value of a technology, unless the technology displays significant and valuable results, it will never take off.
We will use quality of work as a measure of the success of the technology, and differentiate between new and experienced practitioners in determining the quality of work being done. Quality here represents the fraction of projects that are successfully implemented. Projects that lead to bad decisions, are started but abandoned, never get implemented or otherwise get off track are not successes. We will let the quality of work being done influence adoption fraction.
We add new variables to get average quality and its effect on adoption:
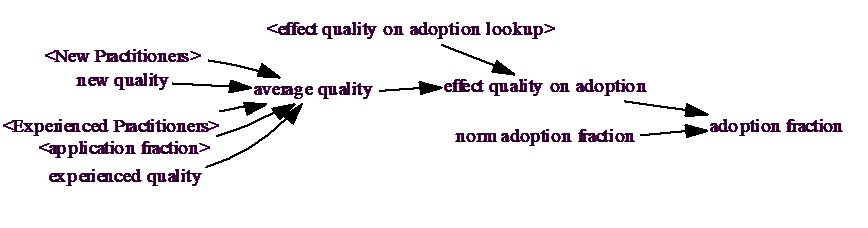
Now we add the equations:
| adoption fraction = norm adoption fraction * |
| effect quality on adoption |
Units: Dmnl
| average quality =XIDZ( New Practitioners * new quality + |
| Experienced Practitioners * application fraction * |
| experienced quality, New Practitioners + |
| Experienced Practitioners * application fraction, |
| experienced quality) |
Units: Dmnl
The XIDZ function prevents a numerical error (overflow) by setting the average quality to experienced quality in the special case when the application fraction is 0.

effect quality on adoption lookup((0,0),(0.8,1))
| effect quality on adoption = effect quality on adoption lookup( |
| average quality) |
Units: Dmnl
experienced quality = 0.8
Units: Dmnl
new quality = 0.4
Units: Dmnl
norm adoption fraction = 0.005
Units: Dmnl
When we simulate this model under the three extremes we get:
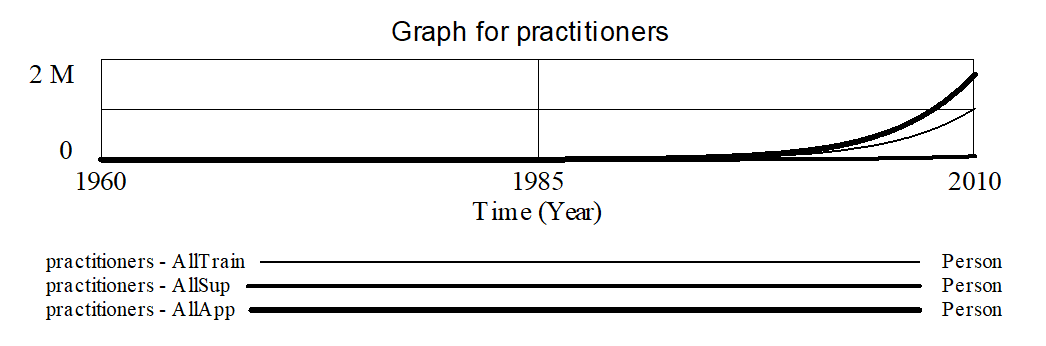
Having all practitioners spend all their time on applications (everyone learns by doing) is now the best growth strategy, but all of the growth rates are slow relative to those of the last model. The reason is simple; when only new practitioners are doing applications the quality is low and new interest is lowered. To maximize growth in this model it is necessary to get a balance between applications and teaching.
If we set both supervision fraction and training fraction to 0.1 we get better results:
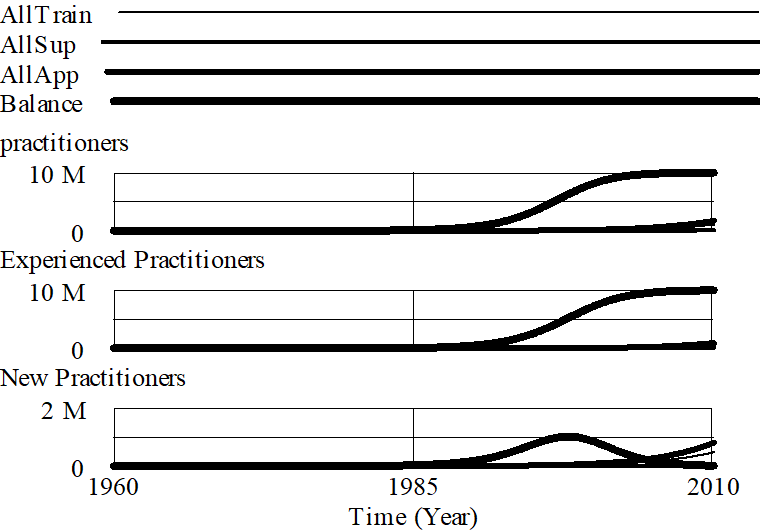
The point here is that as we add additional structure to the model to enhance its realism, the simple-minded strategy of training people like mad falls apart.