A pendulum consists of a weight attached to a string suspended from a hook or other solid attachment. It is a common and well understood device that has been in used in clocks for several centuries. The reason that pendulums are valuable for time keeping is that they maintain a relatively constant period so long as their range of motion is small.
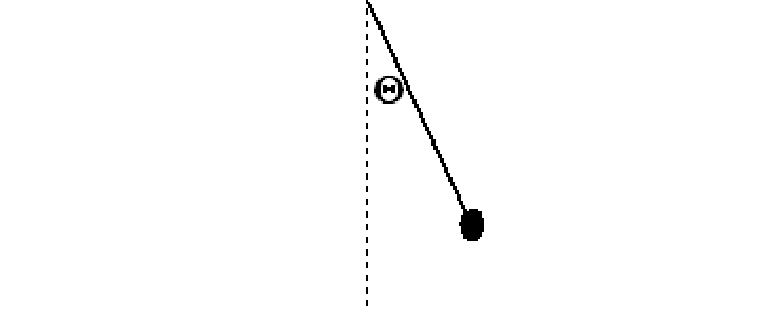
If we let Θ represent the deviation of the pendulum from straight up and down, then the force on the pendulum can be decomposed into a component parallel to the string (mg cos(Θ), where m is the pendulum mass and g is the acceleration of gravity) and a component perpendicular to the string (mg sin(Θ) ). Since the weight can only move perpendicular to the string, the accelerating force is perpendicular to the string, so that the linear acceleration is just g sin(Θ). We can convert this linear acceleration to a radial acceleration by dividing by the length of the string.
We represent this physical problem with the diagram:

Notice the cascaded levels. The acceleration of an object changes its velocity, which in turn changes its position. This means that there is a rate which is also a level. Though this makes good sense for this example, such a situation is actually quite rare for nonphysical models. In the Workforce-Inventory example Inventory is analogous to Angular Position, and Workforce is analogous to Angular Acceleration. In that case, however, Workforce does not directly cumulate into Inventory, but is instead responsible for a process (production) that cumulates into Inventory, all of which introduces more loops as discussed in Chapter 1. This model has only a single feedback loop.
For simplicity, this model uses angles computed in degrees. radian2degree is a constant (=360/2π) that converts between radians and degrees, and is used in the computation of sin(Θ). To maintain dimensional consistency within the equations the unit of measure Radian is considered to be equivalent to dimensionless.
The equations for this model are:
Angular Position = INTEG(Angular Velocity,initial angular position)
Units: Degree
Angular Velocity = INTEG(angular acceleration,0)
Units: Degree/Second
angular acceleration = -radian2degree*
SIN(Angular Position/radian2degree) * g / length
Units: Degree/Second/Second
In this equation you will notice that Angular Position is converted from degrees to radians by dividing by radian2degree. The result (-sin(Θ) g/length) is then in radians and is converted back to degrees by multiplying by radian2degree.
g = 9.2
Units: Meter/Second/Second
initial angular position = 20
Units: Degree
length = 0.5
Units: Meter
radian2degree=57.296
Units: Degree