Vensim Help

If you have ever solved the equations of motion for a pendulum all of the above should seem very familiar with one exception.  Normally the simplifying assumption sin(Θ)=Θ is made.  Because we are simulating these equations, rather than solving them explicitly, the simplification is not necessary.  In fact, we can use this model to understand the implications of larger swings on the period of the pendulum, something that is not possible if the equations are simplified.

Euler Integration

We want to simulate this model for 10 seconds at intervals of 1/32nd of a second (.03125 seconds).  If you attempt this using Euler integration you will get the surprising result:

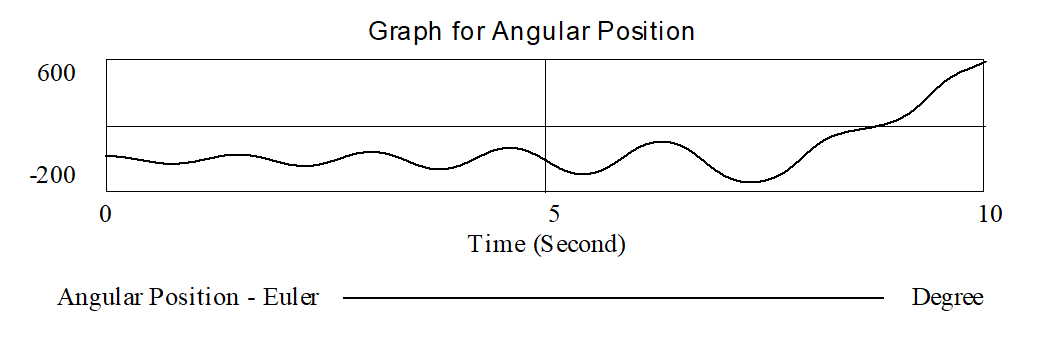
If you are puzzled, this graph says that if you raise the weight to 20 degrees and let go, the pendulum goes back and forth a few times, and then begins to spin around its axis.  While this may be consistent with a child's notion of how a swing ought to work, you would be hard pressed to design a pendulum to do this.  Something is wrong, and it has to do with integration.

When you are using Euler integration and suspect that it is giving bad results, a good test is to cut the integration period in half, and see if the results change.  We can do this by making the simulation run Euler and changing TIME STEP to .015625.:

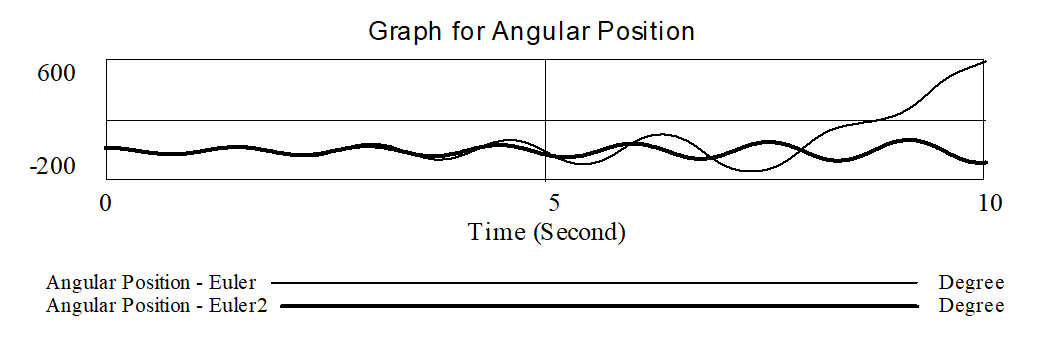
The results change a great deal, but still do not make sense.  The oscillations are still growing, and rotation would likely result in a few more seconds.

In order to get good results from this model using Euler integration you need to make TIME STEP very small indeed (< .001).  If you do want to try this be sure to change SAVEPER to be a number (.0625 or .03125) or Vensim will try to store 10,000 values for each variable and, most likely, fail to do so.  There is, however, a better solution.

The reason that Euler integration fails for this model is that this model represents an undamped oscillator on the edge between stability and instability.  Euler integration is a simple linear extrapolation method, and when you try to extrapolate for something on a curve, you always overshoot the turning point.  Normally a small overshoot is not much cause for concern, but in this case it provides a little bit extra displacement on each cycle, and that adds up to give complete divergence.  

Runge-Kutta Integration

Vensim provides alternative integration techniques for dealing with models such as this.  These methods, referred to as Runge-Kutta Integration, provide higher order extrapolation, looking at both the trajectory and how the trajectory is changing to give a better solution.  

The different choices under Runge-Kutta are RK4 Auto, RK4 Fixed, RK2 Auto and RK2 fixed.  These use higher order approximation (2nd and 4th) to the underlying continuous system.  In general, RK4 Auto is the most accurate technique to use.  It performs, automatically, the experiment of decreasing TIME STEP as done above to check accuracy.  If accuracy is below an acceptable tolerance, the integration interval is decreased further until the desired accuracy is obtained.  This is not always possible, and you will sometimes receive warning messages about being unable to achieve the desired accuracy.  RK4 Fixed is the same as RK4 Auto except that it does not do this accuracy checking.  RK4 Fixed is faster, but you need to test, just as you do for Euler, to see if  accuracy is a problem.

It is important to note that when you are using the Runge-Kutta integration techniques you will not see all intermediate computations. TIME STEP, and therefore normally SAVEPER are not affected by the integration technique.  With any of the Runge-Kutta integration techniques there will always be computations made between TIME STEPS.  You can, consequently, see a level that does not seem to be the accumulation of its inflows and outflows.  For truly continuous systems this will not matter, but if there is any switching going on things can get very confusing.

For small models it is best to use RK4 Auto.  The other integration techniques are intended to allow you to trade off accuracy and simulation time to fit your needs.  When you simulate this model using RK4 Auto you get the results:

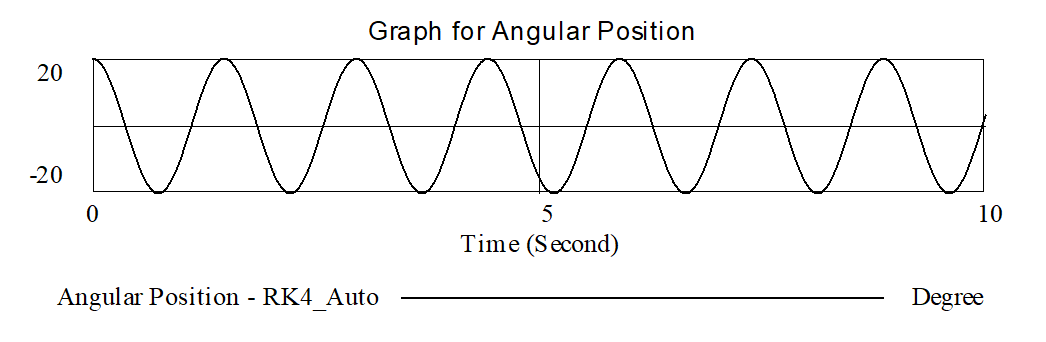
This is more like what you would expect - continued oscillation to plus and minus 20 degrees.  Changing the initial position to 45 degrees (no longer a small deviation) gives:

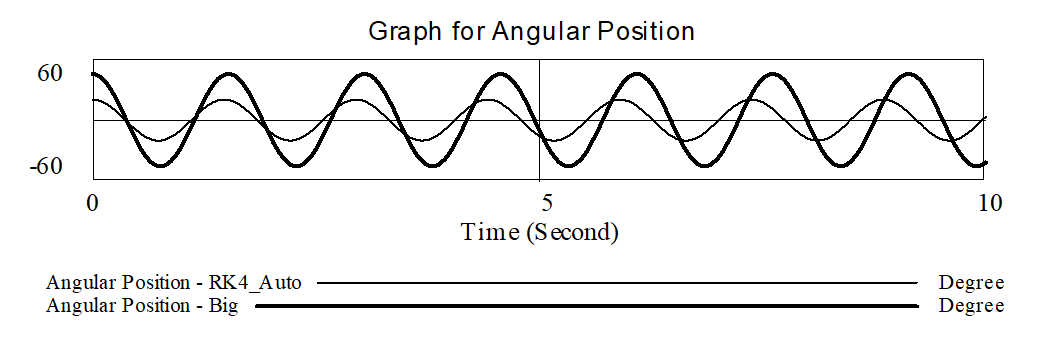
You get the same qualitative behavior, but the period is longer.  This is different from what is typically learned in introductory physics, in which the period is constant due to the approximation of sin(Θ)=Θ.  You might change the model so that:

and see what behavior results.