Equation 4 shows that the values of the Levels and Auxiliaries depend on each other at initialization time. Equation 3 shows that the values of Auxiliaries depend on other Auxiliaries at all times. Both of these equations must satisfy the additional restriction that the value of any given variable at a particular time cannot depend on itself. The value of a variable can, however, depend upon its value at a previous time. A model in which the value of a variable at a particular time can be determined without reference to that variable is said to be causal.
As an example of a model that is not causal, consider a company that attempts to set price in order to achieve a revenue goal. You could represent this as:

If sales change as soon as price does, price changes as soon as indicated price does, and indicated price changes as soon as sales does, then sales effectively depends on itself. Such a system is not causal, and although a mathematical solution to the problem might exist, Vensim will report this as an error and make no attempt to solve it (see Errors).
In this simple example, causality can be restored by recognizing that indicated priceis not adjusted based on current sales, but rather on average sales over the previous weeks, months, or even years.
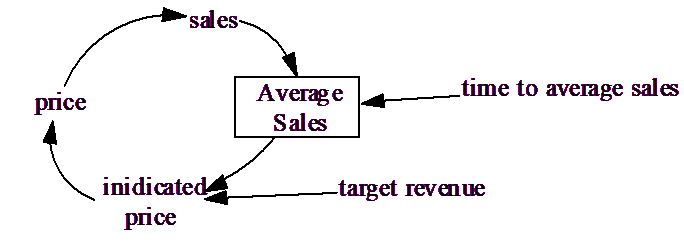
In the above diagram, a box is used to show that Average Sales is a Level variable. Because Average Sales is a Level, its value at a particular time is known as a result of integration from previous times. All feedback loops require at least one Level. (The exception to this rule is that you can use the SIMULTANEOUS or FIND ZERO function to solve a model such as the first one shown. Whether or not simultaneous circular causality constitutes feedback is a question we will leave open.)