1.As a standalone method (Preferred)
Specify MCMC as the OPTIMIZER in your control file, and set any or all options.
MCMC
:OPTIMIZER=MCMC
:MCLIMIT=0
:MCBURNIN=2000
< … model parameter list, e.g.
-5.12<=x[i]<=5.12 … >
Simulated Annealing
:OPTIMIZER=MCMC
:MCTEMP=100
:MCFTEMP=1
:MCLIMIT=0
:MCBURNIN=0
:MCSCHEDULE=2
:MCCOOLING=10000
< … model parameter list, e.g.
-5.12<=x[i]<=5.12 … >
Options
The options, with their default values after the = sign, are as follows:
Iteration Control
:MCLIMIT=0 is the maximum number of iterations to perform. If MCLIMIT<=0, the algorithm runs until stopped by the user.
:MCBURNIN=0 is the number of iterations of the “burn-in period,” during which:
•accepted points are not recorded (to prevent recording of bad points at initialization, before the Markov chains are in steady state).
•outliers are rejected (this cannot be done during an actual MCMC sample because it breaks reversibility or detailed balance).
Chain Control
:MCNCHAINS=2.0 is the number of Markov Chains to run per parameter. So, if you have 6 parameters and MCNCHAINS=2, the algorithm will run 12 chains. The algorithm always runs at least 10 chains. If MCNCHAINS is less than 2, some subspace sampling must be used (MCXOVER > 0). (Note: as of Version 6.3, this is no longer limited to integers, which may be useful for very large parameter sets, where a small value is desirable. However, it's unrealistic to expect truly thorough exploration of large parameter sets by any brute force method.)
:MCOUTLIER=0.05 outlier rejection frequency. This is the fraction of iterations in which chains with outlier payoffs will be rejected. This occurs only during the burnin phase. A rejected chain will be reinitialized to a point near an existing chain.
:MCINITMETHOD=0 method of initializing Markov chains.
•0 chooses a default method: using MCMC as an optimizer, the default method is 0; the default for payoff sensitivity is 3.
•1 overdisperses the starting points, choosing them randomly within the parameter bounds.
•2 underdisperses them, starting as small deviations from the base parameter value in the model (or optimum in the case of payoff sensitivity analysis).
•3 is a hybrid strategy for dispersing points around an optimum, similar to the approach to payoff value sensitivity in Powell optimization. For each chain, a random direction is chosen, and the move in that direction is iteratively scaled by half or doubled until the largest possible move with a reasonable chance of acceptance (5%) is found.
(Note: this differs from the interpretation prior to Version 6.3)
Proposal Generation
:MCGAMMA=1.0 scaling parameter for the determination of proposed points based on directions between current chain states; normally set to 1.
:MCEPSILON=0.01 scaling parameter for multiplicative noise in proposal point generation; normally set to a small value.
:MCDELTA=0.0001 scaling parameter for additive noise in the proposal process; normally set to a small number. If delta is large compared to the yielding "decent" payoffs for a given parameter, chains will have a low acceptance rate, so Delta should be substantially smaller than the smallest parameter range.
:MCJUMP=0.05 the frequency of mode-jumping iterations, in which gamma (see MCGAMMA) is overridden to be equal to 1; normally set to a small number or 0. These occur stochastically, when a random draw on (0,1) is less than MCJUMP.
:MCUPDATEPAIRS=2 number of pairs of chains to combine in differential evolution direction updates. Set to an integer, typically 2 but at least 1. For simulated annealing problems with many local optima, a larger value may be helpful. The value may be set to 0 to effectively skip the evolutionary aspects of the algorithm, performing a pure random walk, but this is unlikely to be efficient in most cases.
:MCXOVER=0.2 frequency of subspace sampling in proposal generation, as a fraction between 0 and 1. With a setting >0, a fraction of proposals will alter only a subset of the full parameter set, effectively slicing a subspace through the full parameter hypercube. (Note: this is the inverse of the interpretation prior to Version 6.3)
Payoff Interpretation
:MCPAYOFFTYPE=0 type of payoff
0 = log likelihood (typical for calibration, also good for arbitrary payoffs as in simulated annealing for policy);
1 = likelihood (this will rarely apply, as log likelihoods are generally more tractable, unless you have problems with log(0), and only if you have created your own explicit expression for the likelihood as a policy payoff). The payoff must be nonnegative for this to make sense.
Output Control
:MCRECORD=0 switch to control reporting of points;
•0 = report all points (necessary if the results are to be interpreted as a sample from a likelihood);
•1 = report only new points from a chain move (which usually will be unique, though duplication is possible).
(Note: this was labeled MCQUNIQUE prior to Version 6.3)
Simulated Annealing
:MCTEMP=1.0 is the initial ‘temperature’ of the system. For pure MCMC, this should be set to 1 unless your likelihood requires scaling. For SA, set this to an estimate of the deepest local minimum, from which you would like the algorithm to (potentially) escape.
:MCFTEMP=1.0 is a floor to temperature. You can set this close to 0 for simulated annealing, or 1 if you wish to anneal first, but finish with MCMC. The floor is not relevant if there is no cooling schedule.
:MCSCHEDULE=0 is the cooling schedule method for SA.
•0 is none (temperature is constant at MCTEMP).
•1 is logarithmic, with temperature = MCTEMP/log(n+i) with n = the number of Markov chains and i = iterations.
•2 is geometric or exponential, with temperature(i) = MCTEMP*exp(-iteration/MCCOOLING).
•3 is linear, with temperature = MCTEMP + (MCFTEMP-MCTEMP)*iteration/MCCOOLING.
(In all cases, temperature respects the MCFTEMP floor).
:MCCOOLING=1000 parameter for cooling schedules 2 and 3, as above, representing the number of iterations over which the cooling occurs. (Note: this is the inverse of the interpretation prior to Version 6.3)
Inherited Options
The seed for the random number generator may be set with :SEED=#, as for the Powell optimizer.
The :SYNTHETIC=# may be set, as for the Powell optimizer.
Note
As of v10.3, we recommend a few changes to earlier default settings:
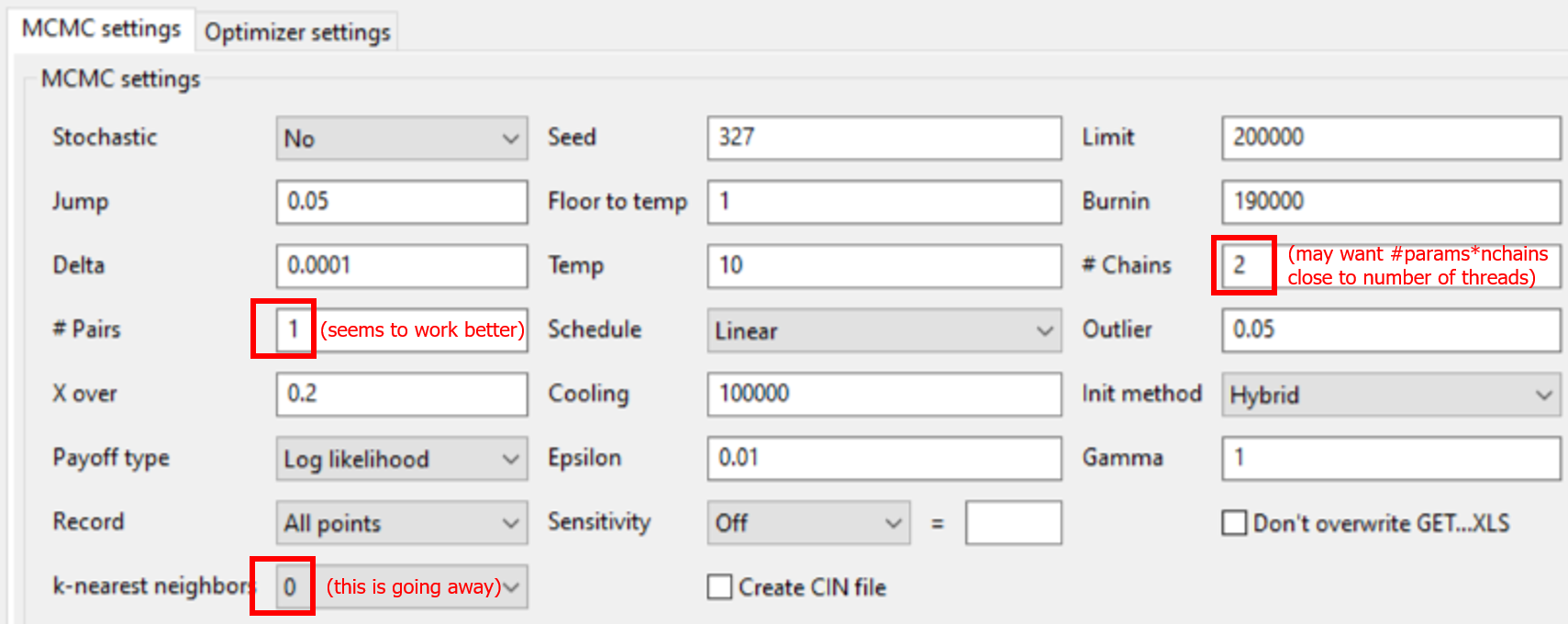
2.As a method of payoff sensitivity analysis in the standard Powell optimizer
To use MCMC this way, specify
:OPTIMIZER=Powell
:SENSITIVITY=PAYOFF MCMC=#value#
:MCLIMIT=10000
<… other Powell or MCMC options and parameters …>
in your optimization control file. You may also include the :MC… parameters described below.
This will cause the optimizer to first run a Powell optimization, then (from the optimum), run the MCMC sensitivity analysis, reporting only points that differ in payoff from the optimum by at most #value# (as with the existing PAYOFF VALUE sensitivity option). MCLIMIT controls the number of iterations. Other :MC keywords may also be used (see below).
The #value# parameter should be chosen on the basis of what the payoff represents.
•If you are using the payoff heuristically, then it is just the range of payoff values that are "interesting" to report.
•If the payoff is a properly weighted sum of squares, it should be distributed Χ2 (Chi squared) with one degree of freedom. Therefore the Χ2 distribution can be used to select an appropriate value, for example 3.84 yields 95% confidence bounds.
•If the payoff is a Normal likelihood, it will include a (sum of squares)/2 term, and therefore half the corresponding Χ2 value should be used. For example, 1.92 yields 95% confidence bounds.
•For other distributions, the appropriate choice may not be obvious, so it may be easier to use standalone MCMC to avoid the decision.
90% |
95% |
99% |
|
Χ2 with 1 DOF |
2.71 |
3.84 |
6.63 |
1/2 Χ2 |
1.36 |
1.92 |
3.32 |